Regularization

正则化(Regularization)是缓解Overfitting非常有效的一项手段，在了解正则化之前，先来看下正则化做了什么：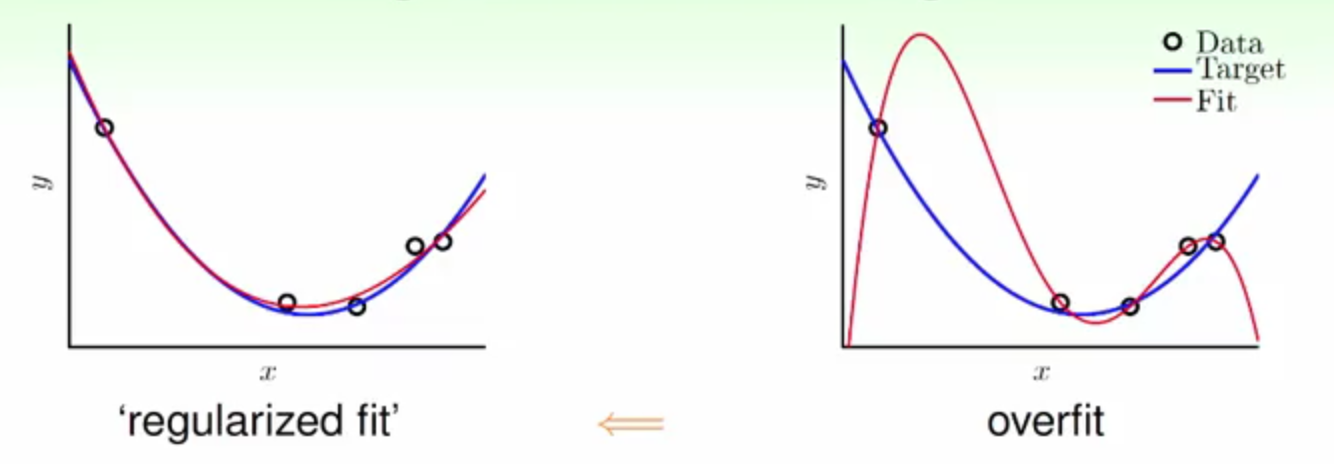

那这种正则化过程又该如何做呢？
其实上面图中的右侧可以看作十次多项式拟合出来的线，而左侧是由二次多项式拟合出得线(这里不了解的点击我)

并且我们还知道低次多项式的假设空间是包含在高次多项式中的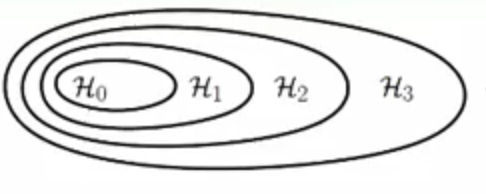

那么也就是说我们如果能把高次的多项式慢慢退回到合适的低次多项式中，就可以缓解Overfitting问题

这里来看一下H2和H10的多项式关系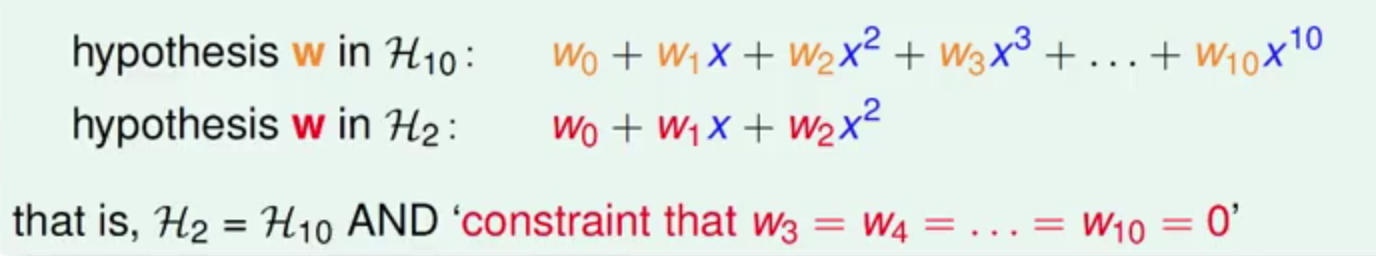

可以发现H2的多项式仅仅是在H10添加了红色的约束即可形成

那这样给我们的启发是在H10多项式退回到H2多项式时可以加约束来操作
现在可以将上述的启发套用到求min(Ein)

1. 上图左侧：求H10的min(Ein)可以按具体模型正常求解,这样相对来说可以得到一个更小的Ein
2. 上图中间：求H2的时候可以在红色约束(后面8个权重值均为0)的基础上求H10的min(Ein)
3. 上图右侧：让约束来的更加宽松一点，只要存在8个权重的值为0，这里可以用H‘2来表示，产生的hypothesis也叫做sparse hypothesis，因为大部分权重值都为0呀^_^

这里就会有：H2 ⊂ H‘2 ⊂ H10

现在看似求解H‘2的min(Ein)即可，但是遗憾的是他是一个NP难题-_-!!
只能继续改进了：原来在H‘2中对不等于0的权重进行计数设定一个阈值，这个过程可以转为将权重平方和小于一个阈值来操作，这样就有了：

这样就转为了一个类似的最佳化问题，并且可以解决原来H‘2离散约束，这个hypothesis叫做H(c),这个H(c)产生的权重要么非常稀疏，要么都是比较小的。
这样产生的权重值叫做Wreg，它也是通过H(c)来完成Regularization的优化解决方案。

现在使用H(c)的求解Linear Regression，将其转为矩阵形式求解为：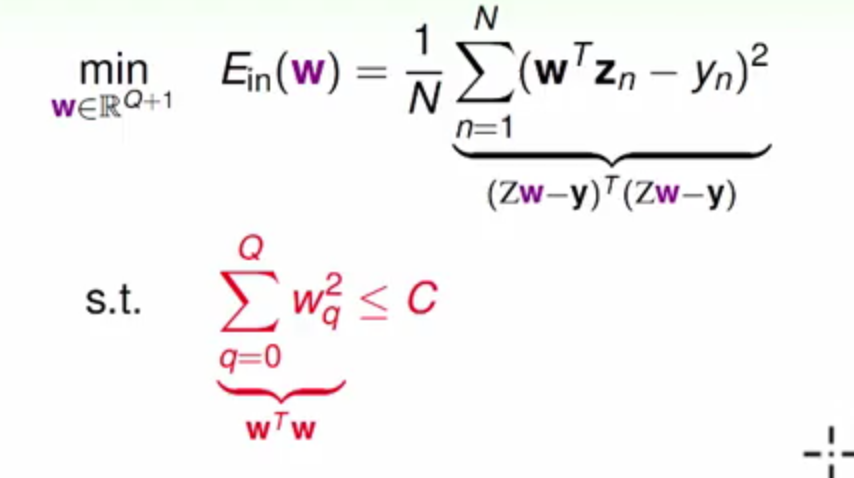

则根据约束条件我们可以知道在约束下最优的解是在半径为sqrt(C)的球里面找到一个权重w使得原始的Ein最小
我们现在需要做的就是在条件下求最佳化问题：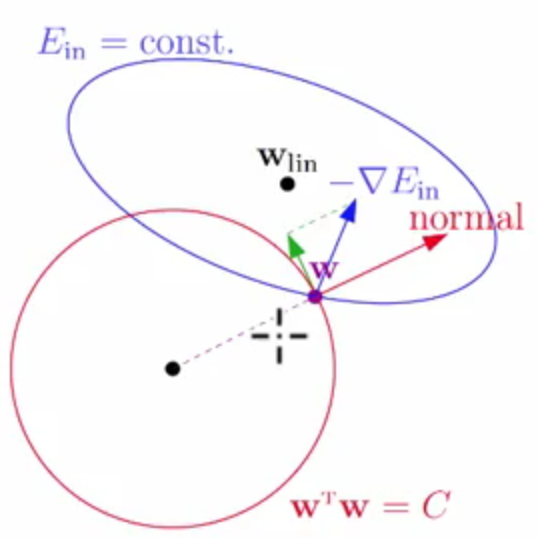

原始问题是沿着梯度反方向滚到谷底即可，也就是椭圆中的Wlin,现在的话该点就会被限制在球内，则我们可以知道最佳点一定是在球的边缘。

则现在w可以滚动的规则为：

1. 球的切面方向量的垂直方向为normal，但是只能往该方向的垂直方向滚动(绿色的向量)，不然就会违背了w在球内的约束条件
2. 要往梯度的反方向滚动(蓝色的方向)，但是为了不违反在球内的条件，所以只能在梯度反方向的分量滚动，并且该方法还必须垂直于normal

所以w滚动的方向是梯度反方向中能垂直球的切面方向量的垂直方向（有点绕。。简单的说，就是蓝色方向与红色垂直的方向滚动），这样即可以满足在球内的约束条件，又可以进一步的优化Ein,直达梯度的反方向与求的切面方向垂直的方向平行，就达到最优了。

因为最终需要那两个方向是平行的，也样通过拉格朗日乘法可以将其写到一个式子里面去

现在假设当前的模型是Linear Regression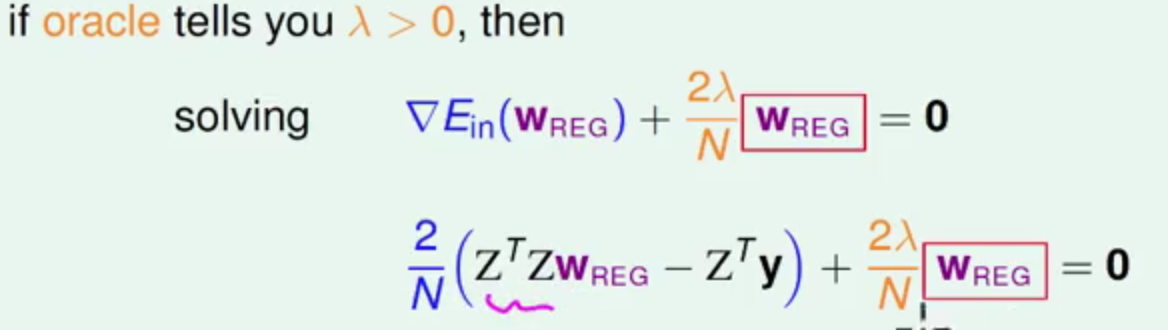

这样只需要求wreg即可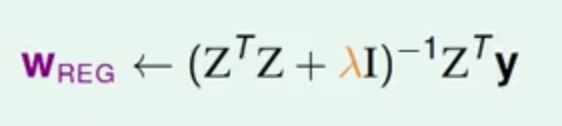

现在延生看待这个问题的话

其中，在原始基础上添加的wTw称作正则项，这里的λ需要取正数大于等于0

这种方式最大的优势就是将原本的阈值C，现在如果知道λ的话就可以在一个式子里面进行直接求解了

关于λ产生的影响的结果图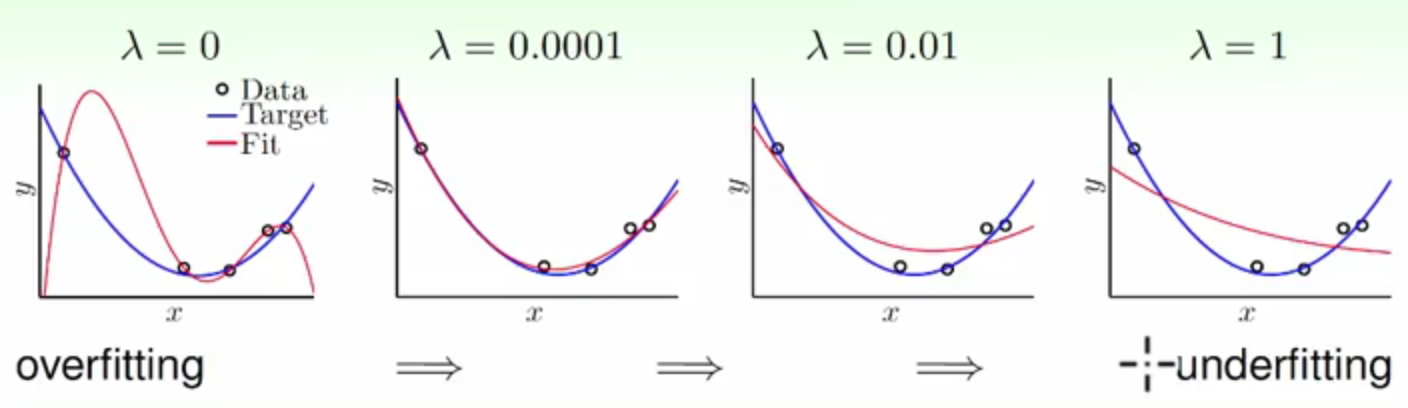

可以发现

1. λ如果不加的会产生Overfitting
2. λ加一点点就可以缓解Overfitting
3. 但是λ加太多的话会产生underfitting

这种正则化的方式叫做weight-decay，会把权重值变小（因为球面上权重向量的各个值都会比较小^_^）。

Regularization and VC theory

通过求带有约束的Ein可以相继得到augmented Error和VC Bound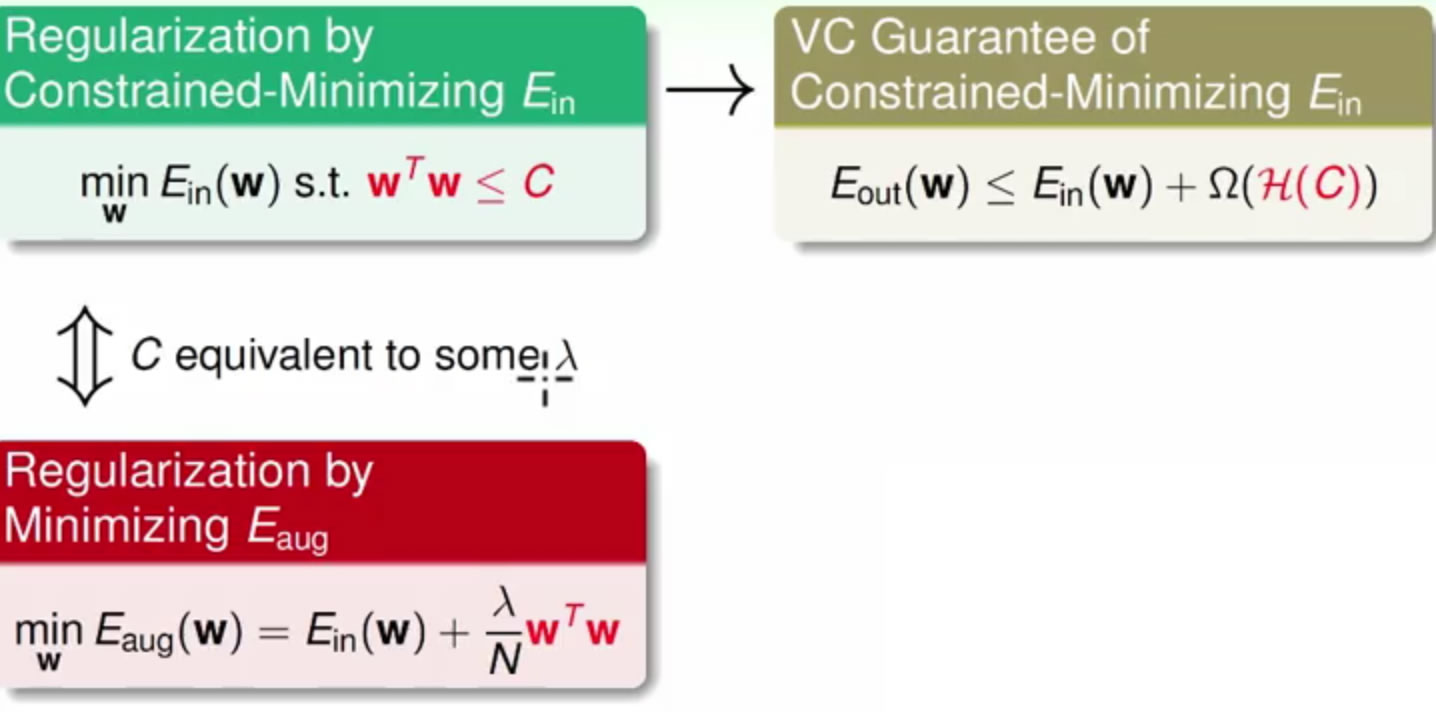

这里在最优化augmented Error的同时其实在间接的求VC Bound

再来看一下他们俩的区别：

• augmented Error它的正则项wTw=Ω(W)是表示一个hypothesis的复杂程度
• VC Bound的Ω(H)是表示整个hypothesis set的复杂程度

那么如果λ/N*Ω(W)与Ω(H)之间存在关联的话，就可以说最小化Eaug是比通过Ein来求Eout的更好的一个代理

再来看具体的一个模型复杂度的一个问题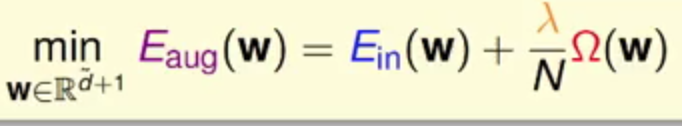

• 原始求Ein他需要的VC复杂度为dvc(H)=d+1，需要在整个hypothesis set中找
• 在Eaug中他是被限制在了H(C)中，所以所需的VC复杂度为dvc(H(C))=dEFF(H,min Eaug),他只考虑了w比较小的情况

所以Eaug有效的VC复杂度要比原来的Ein小很多

L2 VS L1 Regularization

上面提到的||W||2的正则化称为L2 Regulariation,这里再来看一个 L1 Regularization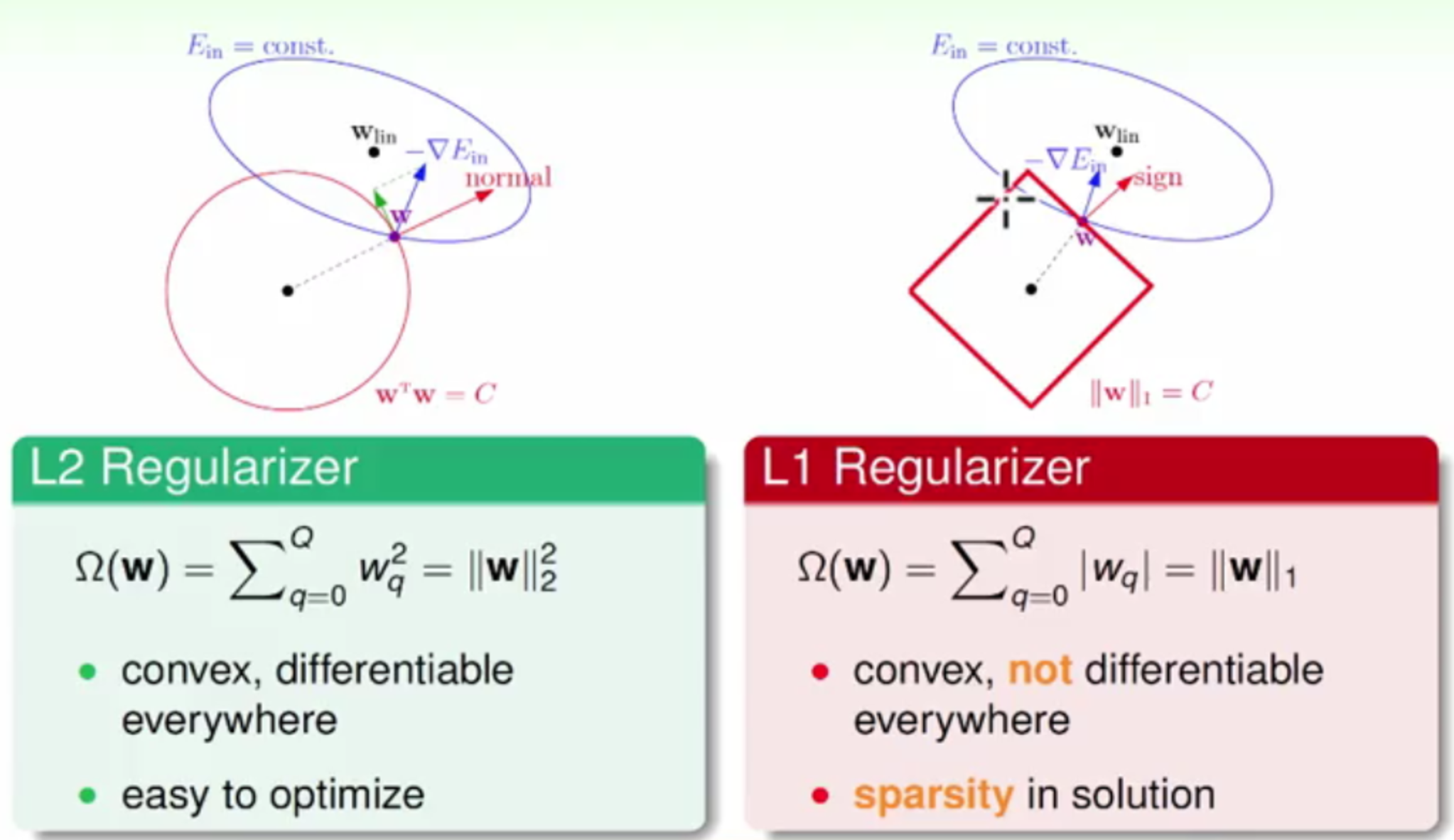

L1 Regularization主要是在原始Ein上添加了权重向量的绝对值求和||W||1,它可以产生更为稀疏的权重值，因为||W||1在多维中可以看做菱形体，根据上面求球体最优的方法，在上面提到的最有约束中我们可以知道w滚动的方向是菱形体法向量垂直的方法（该垂直方向是梯度方向的一个放量），直到滚到菱形体角上的时候，该垂直方向将与梯度方向平行，也就是到了最优，而菱形体角上各个权重的值会是比较稀疏的，也就是说L1 Regularization可以将特征稀疏化（特征稀疏化可以减少存储空间，又可以加快计算速度，只是。。这个稀疏化很不方便优化）。

参考上图对比一下L2 Regulariation和L1 Regulariation：

• L2 Regulariation：凸函数，可以求导，并且很方便优化，最后通过正则化之后得到权重值都会偏小
• L1 Regulariation：凸函数，但是角上无法求导，也就是说优化比较难，通过正则化之后得到的权重值比较稀疏，对于计算和存储都是很大的优势。

关于Eaug中正则项的λ参数的取值最好是按照噪声大小来定^_^

参考

• 《台湾国立大学-机器学习基石》第十四讲

配图均来自《台湾国立大学-机器学习基石》

---

本作品采用[知识共享署名-非商业性使用-相同方式共享 2.5]中国大陆许可协议进行许可，我的博客欢迎复制共享，但在同时，希望保留我的署名权kubiCode，并且，不得用于商业用途。如您有任何疑问或者授权方面的协商，请给我留言。